Understanding Skin Effect and Frequency
The primary bone of contention with my wife is the number of magazines delivered to our house. We get up to 40 different magazines each month. As I'm on-the-road much of the time, I never get a chance to read them all... and so the pile builds. Every so often, I just throw them out unread. I want to read them yet many can be six months or more out of date. Every so often however, I'll pick up one up and read something interesting. Here's a quote from an article on studio installation:
Studio wiring is typically time consuming, complex and represents a good portion of a new studio build expense. Analog cables are susceptible to RFI/EMI emissions and grounding issues. Even the "cleanest" installations cannot avoid cable capacitance or "skin effect" associated with long cable runs that deteriorate signal performance.
And there's a problem here. Back in the old days, when I had more time, I would have been firing off a letter to the editor on this. (Now I can just put it in my blog.) Everything in this quote is true except for one thing: that reference to "skin effect". This unusual effect on wire and cable has been cited so many times by so many people that most readers don't even know what it means. So let me have a go at it.
Skin Effect happens in all wire and cable (or in any metal object that conducts a signal, such as a trace on a circuit board or antennas, etc.). When the "signal" is DC, it uses the entire conductor, with the same amount of current flowing in the center of each wire as on the outside of the wire. As the signal changes frequency (i.e. is now a wave changing direction) a very odd effect occurs: the signal begins to move more to the outside of the conductor than the inside. For audio frequencies, which are pretty low frequencies in the spectrum, this effect is so tiny it can barely be measured. Table 1 below shows how much conductor is used at 20 kHz, pretty much the highest audible frequency, and compares that to various wire sizes. (If you want the actual formula for skin effect, drop me a line and I will send it to you.)
Table 1
|
Basis: |
||||
| Amount of conductor used at 20 kHz, based on conductor size | ||||
| Conductors | Diameter | % of conductor used | ||
| 24 AWG | 0.024 | 100% at 20 kHz | ||
| 22 AWG | 0.031 | 100% at 20 kHz | ||
| 12 AWG | 0.093 | 75% at 20 kHz | ||
| 10 AWG | 0.115 | 68% at 20 kHz | ||
You will notice that even for largest wire size, the difference between the inside and outside of a conductor is a few percentage points. Note that this is based on frequency not on the length of the cable, as mentioned in the quote above. You can see this effect very clearly if you look at the impedance of cables at low frequencies. Figure 2 shows the impedance of a 75 ohm video cable from a frequency of 100 MHz (right margin) down to 10 Hz (left margin).You will see that this 75 ohm cable is really only 75 ohm after around 100 kHz and above. Below that it is way higher than 75 ohms. In fact, down at 10 Hz, the impedance of the cable is around 4,000 ohms.
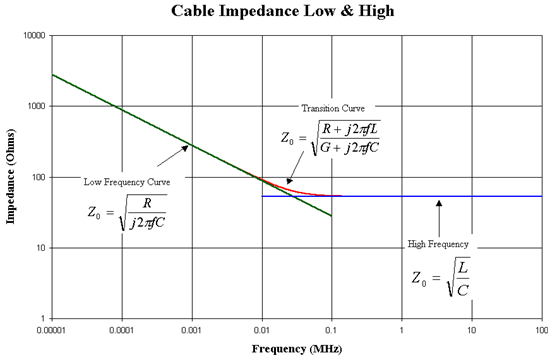
That high-frequency value (75 ohms) is called the "characteristic impedance" of the cable and will stay at 75 ohms (or whatever it was designed to be) out to much higher frequencies. If you compare the low frequency formula to the high-frequency formula, there is one huge difference.R (the resistance of the wire) is a major factor at low frequencies. But in the high frequency formula, there is no R, no resistance. What happened to the resistance? And the answer is "skin effect". As the frequencies got higher and higher, less and less of that conductor is being used, until, around 100 kHz, only the skin is actually carrying the signal.
This is one reason why we can't build an audio cable to a specific impedance. That number will only apply to one frequency. At a different frequency, above or below, the impedance will be a different value. That's why we don't list the impedance of most audio cables and, if we do, that impedance is measured at some high frequency, like 1 MHz, and that cable might be used for some non-audio application. But perhaps you are thinking, "If the resistance of the wire makes no difference, then why won't a small cable go as far as a big cable? "And the answer is equally simple: the big wire has more skin than the small wire.
This is why, when we make cables for high frequencies, we spend a lot of time on the surface of the wire. That's the skin. And at high frequencies, that's the only thing working. So we do a lot of things (many of which are "trade secrets") to make sure the surface of that wire is as perfect as we can possibly make it. Our digital video cables, for instance, are sweep tested and measured out to 4.5 GHz. Signals at these highest frequencies use only micro inches of the outside of the conductor. If all you were carrying was high frequencies, you could use a copper tube as a conductor with no additional loss compared to a solid conductor.
This is why our broadband cables are most often copper clad steel (called "CCS" in our catalog). There's only a thin layer of copper on a steel wire. This means such a cable will only work at high frequencies/And that's OK because TV stations start at Channel 2 which is 54 MHz, well into the skin effect range. (Digital channels now start even higher than that). But someone who uses that cable for low frequencies, such as audio, or to carry DC to power up a satellite dish, will wonder what's wrong with the cable. All the DC power will be going down the steel wire, which is seven times the resistance of copper. What you want for audio or DC power is an all-copper conductor.
Our digital video cables are all-copper, but that's so you can use them for analog or digital video, analog or digital audio, satellite dishes or pretty much any signal at any frequency from DC to 4.5 GHz. Of course copper-clad steel is a lot stronger than bare copper, something that has saved many a CATV/broadband installer who was less than gentle when installing such a cable. So the next time the salesperson is telling you about the "skin effect" in his speaker cable, well, you know the truth!
